Chapter 7 Neural Network
7.1 Neurophysiological Motivation
The original aim of neural network research represented the effort to understand and model how people think and how the human brain functions. The neurophysiological knowledge made the creation of simplified mathematical models possible, which can be exploited in neurocomputing to solve practical tasks from artificial intelligence. This means that the neurophysiology serves here as a source of inspiration and the proposed neural network models are further expanded and refined regardless of whether they model the human brain or not.
The human nervous system intermediates the relationships between the outward environment and the organism itself as well as among its parts to ensure the corresponding response to external stimuli and internal states of the organism, respectively. This process proceeds by transmitting impulses from particular sensors, so-called receptors which enable to receive mechanical, thermal, chemical, and luminous stimuli, to other nervous cells that process these signals and send them to corresponding executive organs, so-called effectors. These impulses passing through the projection channels where the information is preprocessed compressed and filtered for the first time possibly arrive at the cortex that is the top controlling center of the nervous system (see Figure 7.1). On the brain surface about six primary, mutually interconnected projection regions corresponding approximately to senses may be distinguished where the parallel information processing is performed. The complex information processing which is the basis for a conscious controlling of effector activities, proceeds sequentially in so-called associative regions.

Figure 7.1: Block diagram of biological nervous system.
A neuron is a nervous cell, which is the basic functional building element of nervous system. Only the human cortex consists of approximately 13 to 15 billions of neurons which are arranged into a hierarchical structure of six different layers. Moreover, each neuron can be connected with about 5000 of other neurons. The neurons are autonomous cells that are specialized in transmission, processing, and storage of information, which is essential for the realization of vital functions of the organism. The structure of a neuron is schematically depicted in Figure 7.2. The neuron is formed for signal transmission in such a way that, except its proper body, i. e. the so-called soma, it also has the input and output transfer channels, i. e. the dendrites and the axon, respectively. The axon is branched out into many, so-called terminals, which are terminated by a membrane to contact the thorns of dendrites of other neurons as it is depicted in Figure 7.3. A synapse serves as a unique inter-neuron interface to transfer the information. The degree of synaptic permeability bears all-important knowledge during the whole life of the organism. From the functional point of view, the synapses are classified in two types: the excitatory synapses which enable impulses in the nervous system to be spread and the inhibitory ones, which cause their attenuation (see Figure 7.4). A memory trace in the nervous system probably arises by encoding the synaptic bindings on the way between the receptor and effector.
The information transfer is feasible since the soma and axon are covered with a membrane that is capable to generate an electric impulse under certain circumstances. This impulse is transmitted from the axon to dendrites through the synaptic gates whose permeabilities adjust the respective signal intesities. Then each postsynaptic neuron collects the incoming signals whose postsynaptic intensities after being summed up, determine its excitation level. If a certain excitation boundary limit, so-called threshold, is reached, this neuron itself, produces an impulse and thus, the further propagation of underlying information is ensured. During each signal transit, the synaptic permeabilities as well as the thresholds are slightly adapted correspondingjy to the signal intensity, e.g. either the firing threshold is being lowered if the transfer is frequent or it is being increased if the neuron has not been stimulated for a longer time. This represents the neuron plasticity, i.e. the neuron capability to learn, and adapt to varying environment. In addition, the inter-neuron connections are subjected to this evolution process during the organism life. This means that during learning new memory traces are established or the synaptic links are broken in the course of forgetting.
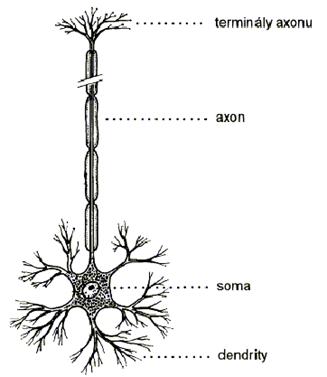
Figure 7.2 : Biological structure of a neureon.

Figure 7.3 : Biological neural network.
At the early stage of the human brain development (the first two years from birth) about 1 million synapses (hard-wired connections) are formed per second. Synapses are then modified through the learning process (plasticity of a neuron). In an adult brain plasticity may be accounted for by the above two mechanisms: creation of new synaptic connections between neurons, and modification of existing synapses.
The human nervous system has a very complex structure, which is still being intensively investigated. However, the above-mentioned oversimplified neurophysiological principles will be sufficient to formulate a mathematical model of neural network.

Figure 7.4 : Functional classification of synapses. A synapse is classified as excitory if a corresponding weight is positive (wi<0) and as inhibitory, if a corresponding weight is negative (wi>0).
7.2 Mathematical Model of Neural Network
A formal neuron, which is obtained by re-formulating a simplified function of biological neuron into a mathematical formalism, will be the basis of the mathematical model of neural network. Its schematic structure (signal-flow graph) is shown in Figure 7.5.
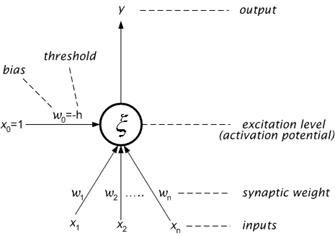
Figure 7.5 : Structure of a formal neuron.
The formal neuron has n, generally real, inputs x1, x2… xn that model the signals coming from dendrites. The inputs are labeled with the corresponding, generally real, synaptic weights w1, w2… wn that measure their permeabilities. According to the neurophysiological motivation, some of these synaptic weights may be negative to express their inhibitory character. Then, the weighted sum of input values represents the excitation level of the neuron:
![]() (7.1)
(7.1)
The value of excitation level x, after reaching the threshold h, induces the output y (state) of the neuron which models the electric impulse generated by axon. The non-linear grow of output value y = s(x) after the threshold excitation level h is achieved, is determined by the activation (transfer, squashing) function s. The simplest type of activation function is the hard limiter, which is of the following form:
![]() (7.2)
(7.2)
By a formal manipulation it can be achieved that the function s has zero threshold and the actual threshold with the opposite sign is understood as a further weight, bias w0= -h of additional formal input x0=1 with constant unit value. Then, the mathematical formulation of neuron function is given by the following expression:
![]() (7.3)
(7.3)
The structure of the arficial neuron in Figure 7.5 is represented graphically using signal-flow graph notation. There are also other representations as shown in Figure 7.6.

(a)

(b)
Figure 7.6 : Graphical representations of artifical neuron; (a) Dendritic representation, and (b) block-diagram representation.
7.3 Neural Network
A neural network consists of formal neurons which are connected in such a way that each neuron output further serves as the input of generally more neurons similarly as the axon terminals of a biological neuron are connected via synaptic bindings with dendrites of other neurons. The number of neurons and the way that they are interconnected determine the architecture (topology) of neural network. Regarding their purpose, the input, working (hidden layer, mediate) and output neurons may be distinguished in the network. The input and output neurons represent the receptors and effectors, respectively, and the connected working neurons create the corresponding channels between them to propagate the respective signals. These channels are called paths in the mathematical model. The signal propagation and information processing along a network path is realized by changing the states of neurons on this path. The states of all neurons in the network form the state of the neural network and the synaptic weights associated with all connections represent the configuration of the neural network.
The neural network develops gradually in time, specifically, the interconnections as well as the neuron states are being changed, and the weights are being adapted. In the context of updating, these network attributes in time, it is useful to split the global dynamics of neural network into three dynamics and consider three modes (phases) of network operation: architectural (topology change), computational (state change), and adaptive (configuration change) (see Figure 7.7). This classification does not correspond to neurophysiological reality since in the nervous system all respective changes proceed simultaneously. The above-introduced dynamics of neural network are usually specified by an initial condition and by a mathematical equation or rule that, determines the development of a particular network characteristic (topology, state, configuration) in time. The updates controlled by these rules are performed in the corresponding operational modes of neural network.

Figure 7.7 : Classification of global dynamics. Phases of network operation.
By a concretization of the introduced dynamics, various models of neural networks are obtained which are suitable to solve specific tasks. This means that in order to specify a particular neural network model it suffices to define its architectural, computational, and adaptive dynamics. In the following exposition, general principles and various types of these three dynamics are described which represent the basis for the classification of neural network models.
7.3.1 Architectural Dynamics
The architectural dynamics specifies the network topology and its possible change. The architecture update usually applies within the framework of an adaptive mode in such a way that the network is supplied with additional neurons and connections when it is needed. However, in most cases the architectural dynamics assumes a fixed neural network topology, which is not changed anymore.
Two types of architectures are distinguished: cyclic (recurrent) and acyclic (feedforward) network. In the cyclic topology, there exists a group of neurons in the network, which are connected into a ring cycle. This means that in this group of neurons the output of the first neuron represents the input of the second neuron whose output is again the input for the third neuron, etc. as far as the output of the last neuron in this group is the input of the first neuron. The simplest cycle is a feedback of the neuron whose output serves simultaneously as its input. The maximum number of cycles is contained in the complete topology in which the output of each neuron represents the input for all neurons. An example of a general cyclic neural network is depicted in Figure 7.8 a where all the cycles are indicated. On the contrary, the feedforward neural networks do not contain any cycle and all paths lead in one direction. An example of an acyclic neural network is in Figure 7.8 b where the longest path is marked.


(a) (b)
Figure 7.8 : Example of architectural dynamics: a. cyclic architecture, b. Acyclic architecture.
The neurons in the feedforward networks can always be disjointly split into layers which are ordered (e.g. arranged one over another) so that the connections among neurons lead only from lower layers to upper ones and generally, they may skip one or more layers. Especially, in a multilayered neural network, the zero (lower), input layer consists of input neurons while the last (upper), output layer is composed of output neurons. The remaining, hidden (intermediate) layers contain hidden neurons. The layers are counted starting from zero that corresponds to the input layer, which is then not included in the number of network layers (e.g. a two-layered neural network consists of input, one hidden, and output layer). In the topology of a multilayered network, each neuron in one layer is connected to all neurons in the next layer (possibly missing connections between two consecutive layers might be implicitly interpreted as connections with zero weights). Therefore, the multilayered architecture can be specified only by the numbers of neurons in particular layers, typically hyphened in the order from input to output layer. In addition, any path in such a network leads from the input layer to the output one while containing exactly one neuron from each layer. An example of a three-layered neural network 3-4-3-2 with an indicated path is in Figure 7.9 which, besides the input and output layers, is composed of two hidden layers.

Figure 7.9 : Example of architecture of multilayered (three-layered) neural network 3-4-3-2.
7.3.2 Computational Dynamics
The computational dynamics specifies the network initial state and a rule for its updates in time, providing that the network topology and configuration are fixed. At the beginning of computational mode, the states of input neurons are assigned to the network input and the remaining neurons find themselves in the initial state. All potential network inputs and states form the input and state space of neural network, respectively. After initializing the network state, a proper computation is performed.
Neural networks considered in previous sections belong to the class of static (feedforward) systems which can be fully described by a set of m-functions of n-variables (see Figure 7.10). The defining feature of the static systems is that they are time-independent, current outputs depends only on the current inputs in the way specified by the mapping function. This function can be very complex.
![]()
Figure 7.10 : A static system: y=f(x)
In the dynamic (recurrent, feedback) systems, the current output signals depend, in general, on current and past input signals. There are two equivalent classes of dynamic systems: continuous-time and discrete-time systems. Continuous-time dynamic systems operate with signals which are functions of a continuous variable, that is continuous function of time. A spatial variable can be also used. Continuous-time dynamic systems are described by means of differential equations. The most convenient yet general description uses only first-order differential equations in the following form:
![]() (7.4)
(7.4)
where
![]() (7.5)
(7.5)
is a vector of time derivatives of output signals. In order to model a dynamic system, or to obtain the output signals, the integration operation is required. The dynamic system of eq. 7.5 is illustrated in Figure 7.11. It is evident that feedback is inherent to dynamic systems.

Figure 7.11 : A
continuous-time dynamic system: ![]()
However, in most cases a discrete computational time is assumed. Discrete-time dynamic systems operate with signals which are functions of a discrete variable, but a discrete spatial variable can be also used. At the beginning the network finds itself at time 0 and the network state is updated only at time 1, 2, 3.. . At each such time step one neuron (during sequential computation) or more neurons (during parallel computation) are selected according to a given rule of computational dynamics. Then, each of these neurons collects its inputs, i.e. the outputs of incident neurons, and updates (changes) its state with respect to them. Analogously, discrete-time dynamic systems are described by means of difference equations. The most convenient yet general description uses only first-order difference equations in the following form:
![]() (7.6)
(7.6)
where y(n + 1) and y(n) are the predicted (future) value and the current value of the vector y, respectively. In order to model a discrete-time dynamic system, or to obtain the output signals, we use the unit delay operator, D = z-1 which originates from the z-transform used to obtain analytical solutions to the difference equations. Using the delay operator, we have z-1y(n+1)= y(n) which leads to the structure as in Figure 7.12. Notice that feedback is also present in discrete model..

Figure 7.12 : A
discrete-time dynamic system: ![]()
According to whether the neurons change their states independently on each other or their updating is centrally controlled, the asynchronous and synchronous models of neural networks, respectively, are distinguished. The states of output neurons, which are generally being varied in time, represent the output of neural network, which is the result of computation. Usually, the computational dynamics is considered so that the network output is constant after a while, and thus, the neural network, under computational mode, implements a function in the input space, i.e. for each network input exactly one output is computed. This neural network function is specified by the computational dynamics whose equations are parametrized by the topology and configuration that are fixed during the computational mode. Obviously, the neural network is exploited for proper computations in the computational mode (see Figure 7.13).

Figure 7.13 : Classification of neural network models according to computational dynamics.
The computational dynamics also determines the function of particular neurons whose formal form (mathematical formula) is usually the same for all (non-input) neurons in the network (homogeneous neural network). By now, we have considered only the function given by eq. 7.3, which has been inspired by a biological neuron operation. However, in neural network models, various neuron functions are in general use, which may not correspond to any neurophysiological pattern, but they are designed only by mathematical invention or even motivated by other theories (e.g. physics). For example, instead of weighted sum (eq. 7.1) a polynomial in several indeterminates (inputs) is exploited in higher-order neural networks. On the other hand, sometimes the excitation level corresponds formally to the distance between the input and respective weight vector, etc. In addition, the transfer function is often approximated by a continuous (or differentiable) activation function or replaced by a completely different function. For example, the sigmoid activation functions create a special class of transfer functions. This class includes hard limiter (eq. 7.7), piecewise linear (saturated-linear function) (eq. 7.8), standart sigmoid (logistic function) (eq. 7.9), hyperbolic tangent (eq. 7.10), etc.
![]() hard limiter
(7.7)
hard limiter
(7.7)
 piecewise-linear function
(7.8)
piecewise-linear function
(7.8)
![]() standard
(logistic)sigmoid
(7.9)
standard
(logistic)sigmoid
(7.9)
![]() hyperbolic tangent
(7.10)
hyperbolic tangent
(7.10)
The graphs of these sigmoid functions are drawn in Figure 7.14. Depending on whether the neuron function is discrete or continuous, the discrete and analog models of neural networks, respectively, are distinguished.

Figure 7.14 : Graphs of sigmoid activation function.
7.3.3 Adaptive dynamics
The adaptive dynamics specifies the network initial configuration and the way that the weights in the network are being adapted in time. All potential network configurations form the weight space of neural network. At the beginning of adaptive mode, the weights of all network connections are assigned to the initial configuration (e.g. randomly). After initializing the network configuration, the proper adaptation is performed. Similarly as for the computational dynamics, a model with a continuous-time evolution of neural network weights when the configuration is a (continuous) function of time usually described by a differential equation may generally be considered. However, in most cases a discrete adaptation time is assumed.
As we know, the network function in the computational mode depends on configuration. The aim of adaptation is to find such a network configuration in the weight space that realizes a desired function in the computational mode. The computational mode is exploited for the respective network function computations while the adaptive mode serves for learning (programming) this function. There exist hundreds of successful learning algorithms for various neural network models (see Figure 7.15). For example, the most well-known and widely applied learning algorithm is the backpropagation for multilayered neural network. The neural network learning represents mostly a complex non-linear optimization problem whose solving can be very time-consuming even for small tasks.

Figure 7.15 : Categorisation of learning paradigms.
A neural network has to be configured such that the application of a set of inputs produces (either direct or via a relaxation process) the desired set of outputs. Various methods to set the strengths of the connections exist. One way is to set the weights explicitly, using a priori knowledge. Another way is to train the neural network by feeding it teaching patterns and letting it change its weights according to some learning rule.
The desired network function is usually specified by a training set (sequence) of pairs composed of the network sample input and the corresponding desired output which are called training patterns. The way, in which the network function is described by a training set, models a teacher (supervisor) who informs the adaptive mechanism about the correct network output corresponding to a given sample network input. Therefore, this type of adaptation is called supervised learning. In supervised learning or associative learning, the network is trained by providing it with input and matching output patterns. These input-output pairs can be provided by an external teacher, or by the system, which contains the network (self-supervised). Sometimes, instead of giving the desired network output value associated with a given sample input, a teacher evaluates the quality of actual current responses (outputs) by a mark. This is called reinforcement (graded) learning.
A different type of adaptation is unsupervised learning or self-organization that models the situation when a teacher is not available. In this case, the training set contains only sample inputs and the neural network itself organizes the training patterns (e.g. into clusters) and discovers their global features. In unsupervised learning, an output unit is trained to respond to clusters of pattern within the input. In this method, the system is supposed to discover statistically salient features of the input population. Unlike the supervised learning, there is not any set of categories exist into which the patterns are to be classified. Rather the system must develop its own representation of the input stimuli.
Feedforward supervised networks are typically used for function approximation tasks. Specific examples include linear recursive least-mean-square (LMS) networks, backpropagation networks, and radial basis networks. Feedforward unsupervised networks are used to extract important properties of the input data and to map input data into a “representation” domain. Two basic groups of methods belong to this category are Hebbian networks performing the Principal Component Analysis of the input data, also known as the Karhunen-Loeve Transform, and Competitive networks used to performed Learning Vector Quantization, or tessellation of the input data set. Self-Organizing Kohonen Feature Maps also belong to this group. Feedback networks are used to learn or process the temporal features of the input data and their internal state evolves with time. Specific examples include recurrent backpropagation networks, associative memories, and adaptive resonance networks.
REFERENCES
[1] Sima J. (1998). Introduction to Neural Networks, Technical Report No. V 755, Institute of Computer Science, Academy of Sciences of the Czech Republic
[2] Kröse B., and van der Smagt P. (1996). An Introduction to Neural Networks. (8th ed.) University of Amsterdam Press, University of Amsterdam.
[3] Gurney K. (1997). An Introduction to Neural Networks. (1st ed.) UCL Press, London EC4A 3DE, UK.
[4] Paplinski A.P. Neural Nets. Lecture Notes, Dept. of Computer Sciences and Software Eng., Manash Universtiy, Clayton-AUSTRALIA