Chapter 3 Network Object Reference

 

 

3.1 Introduction to Programming with MATLAB

:

Before starting to examine the neural network programming, it should be very useful,l to review the abbreviations and notations, that are commonly used in MATLAB. Recall the transition from mathematics to MATLAB code given in chapter 2. To change from mathematics notation to MATLAB notation, the user needs to

Change superscripts to cell array indices:

Change subscripts to parentheses indices

Change parentheses indices to a second cell array index: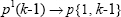

Change mathematics operators to MATLAB operators and toolbox functions: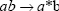

 

3.2 Notation in Functions

 

The notation, that are used in functions and function parameters are listed below.

3.2.1 Dimensions

 

R/Ri Number of input vector elements, that is the input-space dimension 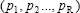( net.inputs{i}.size)

Q Number of concurrent vectors or sequences such as number of input vectors 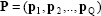such that 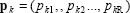(k = 1, 2,…,Q)

Ni Number of network inputs (net.numInputs).

S/Si Number of neurons in layer.(net.layers{i}.size)

Nl Number of layers. (net.numLayers)

Nt Number of targets. (net.numTargets)

Vi Number of elements in target i, equal to Sj, where j is the ith layer with a target. (A layer n has a target if net.targets(n) == 1.)

No Number of network outputs. (net.numOutputs)

Ui Number of elements in output i, equal to Sj, where j is the ith layer with an output (A layer n has an output if net.outputs(n) == 1.)

ID Number of input delays. (net.numInputDelays)

LD Number of layer delays. (net.numLayerDelays)

TS Number of time steps.

 

3.2.2 Variables

 

The variables a user commonly uses when defining a simulation or training session are:

P Network inputs. NixTS cell array, each element P{i,ts} is an RixQ matrix.

Pi Initial input delay conditions. NixID cell array, each element Pi{i,k} is an RixQ matrix.

Ai Initial layer delay conditions. NlxLD cell array, each element Ai{i,k} is an SixQ matrix.

T Network targets. NtxTS cell array, each element P{i,ts} is an VixQ matrix.

These variables are returned by simulation and training calls:

Y Network outputs. NoxTS cell array, each element Y{i,ts} is a UixQ matrix.

E Network errors. NtxTS cell array, each element P{i,ts} is an VixQ matrix.

perf network performance

 

3.2.3 Utility Function Variables

These variables are used only by the utility functions.

Pc Combined inputs. NixID+TS) cell array, each element P{i,ts} is an RixQ matrix. Pc = [Pi P] = Initial input delay conditions and network inputs.

Pd Delayed inputs. NixNjxTS cell array, each element Pd{i,j,ts} is an (Ri*IWD(i,j))xQ matrix, where IWD(i,j) is the number of delay taps associated with input weight to layer i from input j.

Equivalently, IWD(i,j) = length(net.inputWeights{i,j}.delays).

Pd is the result of passing the elements of P through each input weights tap delay lines. Since inputs are always transformed by input delays in the same way it saves time to only do that operation once, instead of for every training step.

BZ Concurrent bias vectors. Nlx1 cell array, each element BZ{i} is a SixQ matrix. Each matrix is simply Q copies of the net.b{i} bias vector.

IWZ Weighted inputs. NixNlxTS cell array, each element IWZ{i,j,ts} is a SixQ matrix.

LWZ Weighed layer outputs. NixNlxTS cell array, each element LWZ{i,j,ts} is a SixQ matrix.

N Net inputs. NixTS cell array, each element N{i,ts} is a SixQ matrix.

A Layer outputs. NlxTS cell array, each element A{i,ts} is a SixQ matrix.

Ac Combined layer outputs. Nlx(LD+TS) cell array, each element A{i,ts} is a SixQ matrix. Ac = [Ai A] = Initial layer delay conditions and layer outputs.

Tl Layer targets. NlxTS cell array, each element Tl{i,ts} is a SixQ matrix. Tl contains empty matrices [] in rows of layers i not associated with targets, indicated by net.targets(i) == 0.

El Layer errors. NlxTS cell array, each element El{i,ts} is a SixQ matrix. El contains empty matrices [] in rows of layers i not associated with targets, indicated by net.targets(i) == 0.

X Column vector of all weight and bias values.

 

3.2.4 Other

 

W         SxR weight matrix (or b, and S x 1 bias vector).

B       Sx1 bias vector (or Nlx1 cell array of bias )

N       SxQ net input vectors.

Z       SxQ weighted input vectors.

PR       Rx2 matrix of min and max values for R input elements.(should contain 2 columns)

A       SxQ output vectors.

T       SxQ layer target vectors.

E       SxQ layer error vectors.

gW       SxR weight gradient with respect to performance.

gA       SxQ output gradient with respect to performance.

D       SxS neuron distances.

LP Learning parameters, none, LP = [].

LS Learning state or new learning state. initially should be = [].

dW SxR weight (or bias) change matrix.

LS New learning state.

TF Transfer function, default = ‘hardlim’.

LF Learning function, default = ‘learnp’.

 

3.3 Network Object Reference

 

The preview of network properties which defines the basic features of a network in this section will be organized as follows:

Architecture: These properties determine the number of network subobjects (which include inputs, layers, outputs, targets, biases, and weights), and how they are connected.

Sub-object structures and properties: These properties consist of cell arrays of structures and their properties that define each of the network’s inputs, layers, outputs, targets, biases, and weights.

Functions: These properties define the algorithms to be used when a network is to adapt, is to be initialized, is to have its performance measured, or is to be trained.

Parameters: These properties define the parameters of a network is to adapt, is to be initialized.

Weight and Bias Values: These properties define the network’s adjustable parameters: its weight matrices and bias vectors.

Other properties.

 

3.4 Network Properties

 

3.4.1 Architecture

The first two properties are numInputs and numLayers. These properties allow us to select how many inputs and layers we want our network to have.

 

 

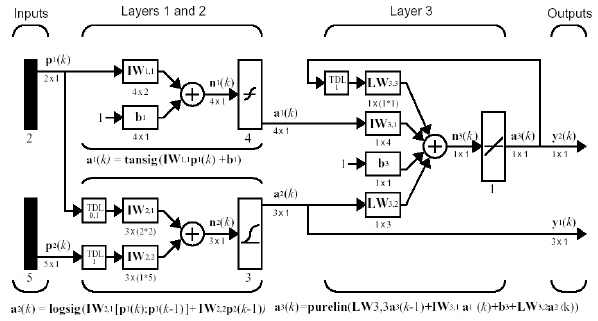
Figure 3.1: The block-diagram of a multi-layer neural network.

 

net.numInputs: This property defines the number of network inputs that is the network receives at a time.

net.numInputs = Ni

The number of network inputs for the network given in Figure 3.1 is:

net.numInputs = 2.

net.numLayers: This property defines the number of layers a network has. It can be set to 0 or a positive integer.

net.numLayers = Nl

The number of layers for the network given in Figure 3.1 is:

net.numLayers = 3.

net.biasConnect: This property defines which layers have biases. It can be set to any Nlx1 matrix of Boolean values. The presence (or absence) of a bias to the ith layer is indicated by a 1 (or 0) at:

net.biasConnect(i)

The bias connections matrix of the neural network given in Figure 3.1 is:

 

 

 

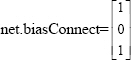
net.inputConnect: This property defines which layers have weights coming from inputs. It can be set to any NlxNi matrix of Boolean values. The presence (or absence) of a weight going to the ith layer from the jth input is indicated by a 1 (or 0) at:

net.inputConnect(i,j)

The input connections matrix of the neural network given in Figure 3.1 is:

 

 

 

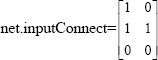
net.layerConnect: This property defines which layers have weights coming from other layers. It can be set to any NlxNl matrix of Boolean values. The presence (or absence) of a weight going to the ith layer from the jth layer is indicated by a 1 (or 0) at:

net.layerConnect(i,j)

The layer connections matrix of the neural network given in Figure 3.1 is:

 

 

 

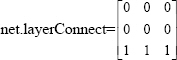
net.outputConnect: This property defines which layers generate network outputs. It can be set to any 1xNl matrix of Boolean values. The presence (or absence) of a network output from the ith layer is indicated by a 1 (or 0) at:

net.outputConnect(i)

The output connections matrix of the neural network given in Figure 3.1 is:

net.outputConnect= [ 0 1 1 ] 

 

net.targetConnect: This property defines which layers have associated targets. It can be set to any 1xNl matrix of Boolean values. The presence (or absence) of a target associated with the ith layer is indicated by a 1 (or 0) at:

net.targetConnect(i)

The target connections matrix of the neural network given in Figure 3.1 is:

net.targetConnect=

net.numOutputs (read-only): This property indicates how many outputs the network has. It is always set to the number of 1’s in the matrix of output connections.

numOutputs = sum(net.outputConnect)

The number of outputs of the neural network given in Figure 3.1 is:

net.numOutputs=2 (Read-only)

 

net.numTargets (read-only):This property indicates how many targets the network has. It is always set to the number of 1’s in the matrix of target connections.

numTargets = sum(net.targetConnect)

The number of targets of the neural network given in Figure 3.1 is:

net.numTargets=1 (Read-only)

 

net. numInputDelays (read-only): This property indicates the number of time steps of past inputs that must be supplied to simulate the network. It is always set to the maximum delay value associated any of the network’s input weights.

 

net.numLayerDelays (read-only): This property indicates the number of time steps of past layer outputs that must be supplied to simulate the network. It is always set to the maximum delay value associated any of the network’s layer weights.

 

3.4.2 Sub-object structures and properties

Inputs

It holds structures of properties for each of the network’s inputs. It is always an Ni x 1 cell array of input structures. The structure defining the properties of the ith network input is located at:

net.inputs{i}

It has

• range,
• size, and 
• userdata

properties explained below.

range: This property defines the ranges of each element of the ith network input. Some initialization functions use input ranges to find appropriate initial values for input weight matrices. It can be set to any Rix2 matrix, where each element in column 1 is less than the element next to it in column 2.

net.inputs{i}.range

Each jth row defines the minimum and maximum values of the jth input element, in that order:

net.inputs{i}(j,:)

 

Specifying range matrix PR

 

The minimum and maximum values for each input vector is specified in a two column matrix PR.

 

size: This property defines the number of elements in the ith network input.

net.inputs{i}.size

Input matrix Pi is a set of RixNi input vectors such that:

 

the size of the network input is;

net.inputs{i}.size=Ri

userdata: This property provides a place for users to add custom information to the ith network input. Only one field is predefined. It contains a secret message to all Neural Network Toolbox users.

net.inputs{i}.userdata.note

Layers

It holds structures of properties for each of the network’s layers. It is always an Nl x 1 cell array of layer structures. The structure defining the properties of the ith layer is located at:

net.layers{i}

It has

• dimensions,
• distanceFcn,
• distances,
• initFcn,
• netInputFcn,
• positions,
• size,
• topologyFcn,
• transferFcn and
• userdata

properties explained below.

dimensions: This property defines the physical dimensions of the ith layer’s neurons. Layer dimensions are used to calculate the neuron positions within the layer (net.layers{i}.positions) using the layer’s topology function (net.layers{i}.topologyFcn). Being able to arrange a layer’s neurons in a multidimensional manner is important for self-organizing maps. It can be set to any row vector of 0 or positive integer elements, where the product of all the elements will becomes the number of neurons in the layer (net.layers{i}.size).

net.layers{i}.dimensions

distanceFcn: Distance functions calculate the distances of a layer’s neurons given their position. This property defines the function used to calculate distances between neurons in the ith layer (net.layers{i}.distances) from the neuron positions (net.layers{i}.positions). Neuron distances are used by self-organizing maps. It can be set to the name of any distance function.

net.layers{i}.distanceFcn

distances (read-only): This property defines the distances between neurons in the ith layer. These distances are used by self-organizing maps. It is always set to the result of applying the layer’s distance function (net.layers{i}.distanceFcn) to the positions of the layers neurons (net.layers{i}.positions).

net.layers{i}.distances

initFcn: The layer initialization function sets all the weights and biases of a layer to values suitable as a starting point for training or adaption. This property defines the initialization function used to initialize the ith layer, if the network initialization function (net.initFcn) is initlay. It can be set to the name of any layer initialization function. If the network initialization is set to initlay, then the function indicated by this property is used to initialize the layer’s weights and biases when init is called net = init(net).

net.layers{i}.initFcn

Layer initialization function returns the network with ith layer's weights and biases updated.

netInputFcn: This property defines the net input function use to calculate the ith layer’s net input, given the layer’s weighted inputs and bias. It can be set to the name of any net input function, including these toolbox functions. The net input function is used to simulate the network when sim is called [Y,Pf,Af] = sim(net,P,Pi,Ai).

net.layers{i}.netInputFcn

Net input functions calculate a layer’s net input vector (or matrix) N, given its weighted input vectors (or matrices) Zi. The only constraints on the relationship between the net input and the weighted inputs are that the net input must have the same dimensions as the weighted inputs, and that the function cannot be sensitive to the order of the weight inputs.

Specifying net input matrix N

The net input matrix N is an SxQ matrix of weighted inputs summed with biases of neurons in the layer such that:

N=W*P + B

 

positions (read-only): This property defines the positions of neurons in the ith layer. These positions are used by self-organizing maps. It is always set to the result of applying the layer’s topology function (net.layers{i}.topologyFcn) to the positions of the layer’s dimensions (net.layers{i}.dimensions). Use plotsom to plot the positions of a layer’s neurons. plotsom(net.layers{1}.positions)

net.layers{i}.positions

size: This property defines the number of neurons in the ith layer. It can be set to 0 or a positive integer.

net.layers{i}.size

The number of neurons in the layers of the neural network given in Figure 3.1 is:

net.layers{1}.size=4, net.layers{2}.size=3, net.layers{3}.size=1

topologyFcn: Topology functions are used in self-organizing maps and calculate the positions of a layer’s neurons given its dimensions. This property defines the function used to calculate the ith layer’s neuron positions (net.layers{i}.positions) from the layer’s dimensions (net.layers{i}.dimensions). It can be set to the name of any topology function. Use plotsom to plot the positions of a layer’s neurons. plotsom(net.layers{1}.positions)

net.topologyFcn

transferFcn: This function defines the transfer function used to calculate the ith layer’s output, given the layer’s net input. It can be set to the name of any transfer function. The transfer function is used to simulate the network when sim is called [Y,Pf,Af] = sim(net,P,Pi,Ai).

net.layers{i}.transferFcn

Transfer functions calculate a layer’s output vector (or matrix) A, given its net input vector (or matrix) N. The only constraint on the relationship between the output and net input is that the output must have the same dimensions as the input.

userdata: This property provides a place for users to add custom information to the ith network layer. Only one field is predefined. It contains a secret message to all Neural Network Toolbox users.

net.layers{i}.userdata

Outputs

It holds structures of properties for each of the network’s outputs. It is always an 1xNl cell array. The structure defining the properties of the output from the ith layer (or a null matrix []) is located at

net.outputs{i}

if the corresponding output connection is 1 (or 0).

net.outputConnect(i)

It has

• size, and
• userdata

properties explained below.

size (read-only): This property defines the number of elements in the ith layer’s output. It is always set to the size of the ith layer (net.layers{i}.size).

net.outputs{i}.size

The size of the outputs of the neural network given in Figure 3.1 is:

net.outputs{1}.size=1, net.outputs{2}.size=3

userdata: This property provides a place for users to add custom information to the ith layer’s output. Only one field is predefined. It contains a secret message to all Neural Network Toolbox users.

net.outputs{i}.userdata.note

Targets

It holds structures of properties for each of the network’s targets. It is always an 1 x Nl cell array. The structure defining the properties of the target associated with the ith layer (or a null matrix []) is located at

net.targets{i}

if the corresponding target connection is 1 (or 0).

net.targetConnect(i)

It has

• size, and
• userdata

properties explained below.

size (read-only): This property defines the number of elements in the ith layer’s target. It is always set to the size of the ith layer (net.layers{i}.size).

net.targets{i}.size

The size of the targets of the neural network given in Figure 3.1 is:

net.targets{3}.size=1

userdata: This property provides a place for users to add custom information to the ith layer’s target. Only one field is predefined. It contains a secret message to all Neural Network Toolbox users.

net.targets{i}.userdata.note

Biases

It holds structures of properties for each of the network’s biases. It is always an Nlx1 cell array. The structure defining the properties of the bias associated with the ith layer (or a null matrix []) is located at

net.biases{i}

if the corresponding bias connection is 1 (or 0).

net.biasConnect(i)

It has

• initFcn,
• learn,
• learnFcn
• learnParam
• size, and
• userdata

properties explained below.

initFcn: The bias initialization function sets all the biases of a bias to values suitable as a starting point for training or adaption. This property defines the function used to initialize the ith layer’s bias vector, if the network initialization function is initlay, and the ith layer’s initialization function is initwb.

net.biases{i}.initFcn

This function can be set to the name of any bias initialization function, including the toolbox functions. This function is used to calculate an initial bias vector for the ith layer (net.b{i}) when init is called, if the network initialization function (net.initFcn) is initlay, and the ith layer’s initialization function (net.layers{i}.initFcn) is initwb.

net = init(net)

learn: This property defines whether the ith bias vector is to be altered during training and adaption. It can be set to 0 or 1.

net.biases{i}.learn

It enables or disables the bias’ learning during calls to either adapt or train.

[net,Y,E,Pf,Af] = adapt(NET,P,T,Pi,Ai)

[net,tr] = train(NET,P,T,Pi,Ai)

learnFcn: The learning functions are used to update individual weights and biases during learning. with some training and adapt functions. This property defines the function used to update the ith layer’s bias vector during training, if the network training function is trainb, trainc, or trainr, or during adaption, if the network adapt function is trains.

net.biases{i}.learnFcn

It can be set to the name of any bias learning function. The learning function updates the ith bias vector (net.b{i}) during calls to train, if the network training function (net.trainFcn) is trainb, trainc, or trainr, or during calls to adapt, if the network adapt function (net.adaptFcn) is trains.

[net,Y,E,Pf,Af] = adapt(NET,P,T,Pi,Ai)

[net,tr] = train(NET,P,T,Pi,Ai)

learnParam: This property defines the learning parameters and values for the current learning function of the ith layer’s bias. The fields of this property depend on the current learning function (net.biases{i}.learnFcn).

net.biases{i}.learnParam

size (read-only): This property defines the size of the ith layer’s bias vector. It is always set to the size of the ith layer (net.layers{i}.size).

net.biases{i}.size

The size of the biases of the neural network given in Figure 3.1 is:

net.biases{1}.size=4, net.biases{3}.size=1

userdata:This property provides a place for users to add custom information to the ith layer’s bias. Only one field is predefined. It contains a secret message to all Neural Network Toolbox users.

net.biases{i}.userdata.note

Input Weights

It holds structures of properties for each of the network’s input weights. It is always an NlxNi cell array. The structure defining the properties of the weight going to the ith layer from the jth input (or a null matrix []) is located at

net.inputWeights{i,j}

if the corresponding input connection is 1 (or 0).

net.inputConnect(i,j)

It has

• delays
• initFcn,
• learn,
• learnFcn
• learnParam
• size,
• userdata, and
• weightFcn
• properties explained below.

delays: This property defines a tapped delay line between the jth input and its weight to the ith layer. It must be set to a row vector of increasing 0 or positive integer values.

net.inputWeights{i,j}.delays

initFcn: The weight initialization function sets all the weights of a weight to values suitable as a starting point for training or adaption. This property defines the function used to initialize the weight matrix going to the ith layer from the jth input, if the network initialization function is initlay, and the ith layer’s initialization function is initwb. This function can be set to the name of any weight initialization function

net.inputWeights{i,j}.initFcn

This function is used to calculate an initial weight matrix for the weight going to the ith layer from the jth input (net.IW{i,j}) when init is called, if the network initialization function (net.initFcn) is initlay, and the ith layer’s initialization function (net.layers{i}.initFcn) is initwb.

net = init(net)

learn: This property defines whether the weight matrix to the ith layer from the jth input is to be altered during training and adaption. It can be set to 0 or 1.

net.inputWeights{i,j}.learn

It enables or disables the weights learning during calls to either adapt or train.

[net,Y,E,Pf,Af] = adapt(NET,P,T,Pi,Ai)

[net,tr] = train(NET,P,T,Pi,Ai)

learnFcn: The learning functions are used to update individual weights and biases during learning. with some training and adapt functions. This property defines the function used to update the weight matrix going to the ith layer from the jth input during training, if the network training function is trainb, trainc, or trainr, or during adaption, if the network adapt function is trains.

net.inputWeights{i,j}.learnFcn

It can be set to the name of any weight learning function. The learning function updates the weight matrix of the ith layer from the jth input (net.IW{i,j}) during calls to train, if the network training function (net.trainFcn) is trainb, trainc, or trainr, or during calls to adapt, if the network adapt function (net.adaptFcn) is trains.

[net,Y,E,Pf,Af] = adapt(NET,P,T,Pi,Ai)

[net,tr] = train(NET,P,T,Pi,Ai)

learnParam: This property defines the learning parameters and values for the current learning function of the ith layer’s weight coming from the jth input.

net.inputWeights{i,j}.learnParam

The fields of this property depend on the current learning function

(net.inputWeights{i,j}.learnFcn).

size (read-only): This property defines the dimensions of the ith layer’s weight matrix from the jth network input.

net.inputWeights{i,j}.size

It is always set to a two-element row vector indicating the number of rows and columns of the associated weight matrix (net.IW{i,j}). The first element is equal to the size of the ith layer (net.layers{i}.size). The second element is equal to the product of the length of the weights delay vectors with the size of the jth input:

length(net.inputWeights{i,j}.delays) * net.inputs{j}.size

The size of the input weights of the neural network given in Figure 3.1 is:

net.inputWeights{1,1}.size=4, net.inputWeights{2,1}.size=3

userdata:This property provides a place for users to add custom information to the (i,j) th input weight. Only one field is predefined. It contains a secret message to all Neural Network Toolbox users.

net.inputWeights{i,j}.userdata.note

weightFcn: Weight functions calculate a weighted input vector (or matrix) Z, given an input vector (or matrices) P and a weight matrix W. This property defines the function used to apply the ith layer’s weight from the jth input to that input. It can be set to the name of any weight function.

net.inputWeights{i,j}.weightFcn

The weight function is used when sim is called to simulate the network.

[Y,Pf,Af] = sim(net,P,Pi,Ai)

Layer Weights

It holds structures of properties for each of the network’s layer weights. It is always an NlxNl cell array. The structure defining the properties of the weight going to the ith layer from the jth layer (or a null matrix []) is located at:

net.layerWeights{i,j}

if the corresponding layer connection is 1 (or 0).

net.layerConnect(i,j)

It has

• delays
• initFcn,
• learn,
• learnFcn
• learnParam
• size,
• userdata, and
• weightFcn

properties explained below.

delays: This property defines a tapped delay line between the jth layer and its weight to the ith layer. It must be set to a row vector of increasing 0 or positive integer values.

net.layerWeights{i,j}.delays

initFcn: The weight initialization function sets all the weights of a weight to values suitable as a starting point for training or adaption. This property defines the function used to initialize the weight matrix going to the ith layer from the jth layer, if the network initialization function is initlay, and the ith layer’s initialization function is initwb.

net.layerWeights{i,j}.initFcn

This function can be set to the name of any weight initialization function, including the toolbox functions. This function is used to calculate an initial weight matrix for the weight going to the ith layer from the jth layer (net.LW{i,j}) when init is called, if the network initialization function (net.initFcn) is initlay, and the ith layer’s initialization function (net.layers{i}.initFcn) is initwb.

net = init(net)

learn: This property defines whether the weight matrix to the ith layer from the jth layer is to be altered during training and adaption. It can be set to 0 or 1.

net.layerWeights{i,j}.learn

It enables or disables the weights learning during calls to either adapt or train.

[net,Y,E,Pf,Af] = adapt(NET,P,T,Pi,Ai)

[net,tr] = train(NET,P,T,Pi,Ai)

learnFcn: The learning functions are used to update individual weights and biases during learning. with some training and adapt functions. This property defines the function used to update the weight matrix going to the ith layer from the jth layer during training, if the network training function is trainb, trainc, or trainr, or during adaption, if the network adapt function is trains.

net.layerWeights{i,j}.learnFcn

It can be set to the name of any weight learning function. The learning function updates the weight matrix of the ith layer form the jth layer (net.LW{i,j}) during calls to train, if the network training function (net.trainFcn) is trainb, trainc, or trainr, or during calls to adapt, if the network adapt function (net.adaptFcn) is trains.

[net,Y,E,Pf,Af] = adapt(NET,P,T,Pi,Ai)

[net,tr] = train(NET,P,T,Pi,Ai)

learnParam: This property defines the learning parameters fields and values for the current learning function of the ith layer’s weight coming from the jth layer.

net.layerWeights{i,j}.learnParam

The subfields of this property depend on the current learning function

(net.layerWeights{i,j}.learnFcn).

size (read-only): This property defines the dimensions of the ith layer’s weight matrix from the jth layer. It is always set to a two-element row vector indicating the number of rows and columns of the associated weight matrix (net.LW{i,j}). The first element is equal to the size of the ith layer (net.layers{i}.size). The second element is equal to the product of the length of the weights delay vectors with the size of the jth layer length(net.layerWeights{i,j}.delays)* net.layers{j}.size

net.layerWeights{i,j}.size

The size of the layers weights of the neural network given in Figure 3.1 is:

net.layerWeights{3,1}.size=1, net.layerWeights{3,2}.size=1, net.layerWeights{3,3}.size=1

userdata This property provides a place for users to add custom information to the (i,j) th layer weight. Only one field is predefined. It contains a secret message to all Neural Network Toolbox users.

net.layerWeights{i,j}.userdata.note

weightFcn: Weight functions calculate a weighted input vector (or matrix) Z, given an input vector (or matrices) P and a weight matrix W. This property defines the function used to apply the ith layer’s weight from the jth layer to that layer’s output.

net.layerWeights{i,j}.weightFcn

It can be set to the name of any weight function. The weight function is used when sim is called to simulate the network.

[Y,Pf,Af] = sim(net,P,Pi,Ai)

 

3.4.3 Functions

net.adaptFcn: Adapt functions simulate a network, while updating the network for each time step of the input before continuing the simulation to the next input. This property defines the function to be used when the network adapts. It can be set to the name of any network adapt function. The network adapt function is used to perform adaption whenever adapt is called.

[net,Y,E,Pf,Af] = adapt(NET,P,T,Pi,Ai)

net.initFcn: The network initialization function sets all the weights and biases of a network to values suitable as a starting point for training or adaption. This property defines the function used to initialize the network’s weight matrices and bias vectors. It can be set to the name of any network initialization function. The initialization function is used to initialize the network whenever init is called.

net = init(net)

net.performFcn: Performance functions allow a network’s behavior to be graded. This is useful for many algorithms, such as backpropagation, which operate by adjusting network weights and biases to improve performance. This property defines the function used to measure the network’s performance. It can be set to the name of any performance function. The performance function is used to calculate network performance during training whenever train is called.

[net,tr] = train(NET,P,T,Pi,Ai)

net.trainFcn: Training functions repeatedly apply a set of input vectors to a network, updating the network each time, until some stopping criteria is met. Stopping criteria can consists of a maximum number of epochs, a minimum error gradient, an error goal, etc. This property defines the function used to train the network. It can be set to the name of any training function. The training function is used to train the network whenever train is called.

[net,tr] = train(NET,P,T,Pi,Ai)

 

3.4.4 Parameters

net.adaptParam:This property defines the parameters and values of the current adapt function. The fields of this property depend on the current adapt function.

net.initParam:This property defines the parameters and values of the current initialization function. The fields of this property depend on the current initialization function.

net.performParam :This property defines the parameters and values of the current performance function. The fields of this property depend on the current performance function

net.trainParam: This property defines the parameters and values of the current training function. The fields of this property depend on the current training function.

 

3.4.5 Weight and Bias Values

net.IW: This property defines the weight matrices of weights going to layers from network inputs. It is always an NlxNi cell array. The weight matrix for the weight going to the ith layer from the jth input (or a null matrix []) is located at net.IW{i,j} if the corresponding input connection is 1 (or 0). net.inputConnect(i,j) The weight matrix has as many rows as the size of the layer it goes to (net.layers{i}.size). It has as many columns as the product of the input size with the number of delays associated with the weight.

net.inputs{j}.size * length(net.inputWeights{i,j}.delays)

These dimensions can also be obtained from the input weight properties.

net.inputWeights{i,j}.size

Specifying input weight matrix net.IW

The weight matrix W is a set of vectors that is related for each neuron in the current layer. Since the weight matrix is SixRi the rows are related with neurons and the columns are related with inputs as:

 

The input weights of a network with two network input and two layers where the network input 1 is connected with layer 1 but not with layer 2 and network input 2 is connected with layer 2 and layer 1 is represented as

 

net.LW: This property defines the weight matrices of weights going to layers from other layers. It is always an NlxNl cell array. The weight matrix for the weight going to the ith layer from the jth layer (or a null matrix []) is located at net.LW{i,j} if the corresponding layer connection is 1 (or 0). net.layerConnect(i,j) The weight matrix has as many rows as the size of the layer it goes to (net.layers{i}.size). It has as many columns as the product of the size of the layer it comes from with the number of delays associated with the weight.

net.layers{j}.size * length(net.layerWeights{i,j}.delays)

These dimensions can also be obtained from the layer weight properties.

net.layerWeights{i,j}.size

Specifying layer weight matrix net.LW

The weight matrix W is a set of vectors that is related for each neuron in the current layer. Since the weight matrix is SixRi the rows are related with neurons and the columns are related with inputs coming from other layers as:

 

The input weights of a network with two layers where the layer 1 is connected with layer 2 and layer 2 has a cyclic nature that is, it has a feedback to itself is represented as

 

net.b: This property defines the bias vectors for each layer with a bias. It is always an Nlx1 cell array. The bias vector for the ith layer (or a null matrix []) is located at net.b{i} if the corresponding bias connection is 1 (or 0).

net.biasConnect(i)

The number of elements in the bias vector is always equal to the size of the layer it is associated with (net.layers{i}.size). This dimension can also be obtained from the bias properties.

net.biases{i}.size

Specifying network bias matrix net.b

The bias matrix B is an S x 1 array of biases of neurons in the layer such that:

 

Other

net.userdata: This property provides a place for users to add custom information to a network object. Only one field is predefined. It contains a secret message to all Neural Network Toolbox users.

net.userdata.note

 

3.4.6 Other Issues

 

Specifying input matrix P

Input matrix P is a set of R x Q input vectors such that:

 

Thus the columns of the matrix are vectors, and the rows are the components of the vectors.

 

Specifying weighted input matrix Z

The weighted input matrix Z is an S x Q matrix of weighted inputs with biases included of neurons in the layer such that:

Z=W*P

 

Specifying output matrix A

For each input vector , the outputs of the neurons in the layer are calculated by the neuron functions such that

 

Since the output vectors are computed by the system it should be initialized to empty matrix [].

Specifying layer target matrix T

For each input vector , the desired output matrix T of the neurons in the layer are specified such that

 

 

REFERENCES

[1] Demuth H., and Beale M. (2003). Neural Network Toolbox For Use With MATLAB, User’s Guide, Mathworks Inc., version 4.0